Teori Dasar Himpunan dan Beberapa Contoh Soal
Himpunan adalah sekelompok obyek yang mempunyai sifat keterlibatan yang sama dan dapat dibedakan antara obyek yang satu dengan lainnya. Suatu himpunan biasanya dilambangkan dengan menggunakan huruf besar, misalnya A,B,C, . . ., sedangkan unsur suatu himpunan dituliskan dengan huruf kecil seperti a,b,c,x,y,...
1. Cara pendaftaran (Roster Method)
Pada cara ini, unsur himpunan didaftarkan satu persatu, misalnya :
$ A = \left \{ x_{1},x_{2},x_{3},...,x_{n} \right \} $
2. Cara perincian (Rule Method)
Pada cara ini, unsur himpunan dituliskan atas dasar sifat unsur tersebut, umumnya
penulisan pada cara ini ialah $ A = \left \{ x \mid sifat-sifat\ dari\ x \right \} $
anggota†dari suatu himpunan.
Contoh :
$ 1.\ A = \left \{ 1, 2, 3 \right \} maka\ 1\in A ; 2\in A ; 3\in A ; 0\notin A ; \left \{1 \right \}\notin A ; 4\notin A.$
$ 2.\ B = \left \{ x \mid x^{2}-x-6=0,\ x\in asli \right \}, maka\ 3\in B\ tetapi\ -2\notin B$
Himpunan yang tidak mempunyai anggota dinamakan himpunan kosong (empty set) ditulis $ \left \{ \ \right \} $ atau $\varnothing $, misalnya :
$ 1.\ A = \left \{ x \mid x^{2}+5x+6=0,\ x\in asli \right \}, maka\ A = \varnothing = \left \{ \ \right \}$
Sifat :
1. ∅ ⊂ A , A himpunan sembarang
2. A ⊂ B dan B ⊂ C ⇒ A ⊂ C










Contoh:






Contoh:








Demikian penjelasan sederhana tentang teori dasar himpunan dan beberapa contoh soal dan pembahasan yang sudah pernah dikeluarkan dalam seleksi masuk perguruan tinggi negeri.
Via : http://www.foldersoal.com
Suatu himpunan, dapat dituliskan dengan dua cara, yaitu :Cara Penulisan Himpunan
Pada cara ini, unsur himpunan didaftarkan satu persatu, misalnya :
Baca Juga
2. Cara perincian (Rule Method)
Pada cara ini, unsur himpunan dituliskan atas dasar sifat unsur tersebut, umumnya
penulisan pada cara ini ialah $ A = \left \{ x \mid sifat-sifat\ dari\ x \right \} $
Untuk menyatakan suatu unsur merupakan “anggota“ pada suatu himpunan digunakan lambang “ $ \in $ †, sedangkan lambang “ $ \notin $ “ digunakan menyatakan “bukanKeanggotaan Himpunan
Contoh :
$ 1.\ A = \left \{ 1, 2, 3 \right \} maka\ 1\in A ; 2\in A ; 3\in A ; 0\notin A ; \left \{1 \right \}\notin A ; 4\notin A.$
$ 2.\ B = \left \{ x \mid x^{2}-x-6=0,\ x\in asli \right \}, maka\ 3\in B\ tetapi\ -2\notin B$
Himpunan yang tidak mempunyai anggota dinamakan himpunan kosong (empty set) ditulis $ \left \{ \ \right \} $ atau $\varnothing $, misalnya :
$ 1.\ A = \left \{ x \mid x^{2}+5x+6=0,\ x\in asli \right \}, maka\ A = \varnothing = \left \{ \ \right \}$
Definisi: Himpunan A dikatakan himpunan bagian dari B jika dan hanya jika untuk setiap $ x\in A\ maka\ x\in B\ ditulis\ A \subset B$Himpunan Bagian
Sifat :
1. ∅ ⊂ A , A himpunan sembarang
2. A ⊂ B dan B ⊂ C ⇒ A ⊂ C





Operasi pada Himpunan

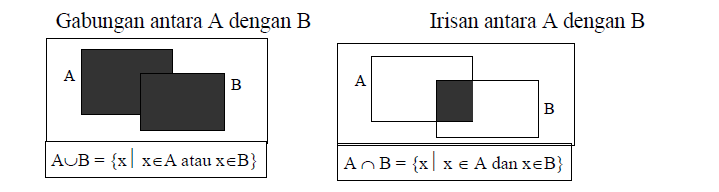
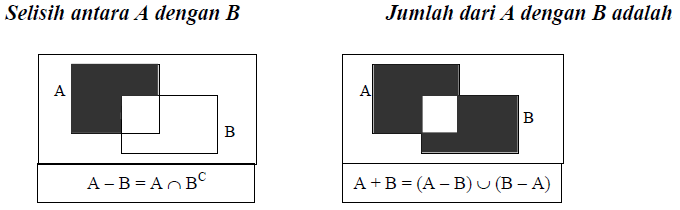

Contoh:





Bilangan kardinal dari A adalah bilangan cacah yang menyatakan banyaknya unsur dari A, ditulis n(A).Bilangan Kardinal
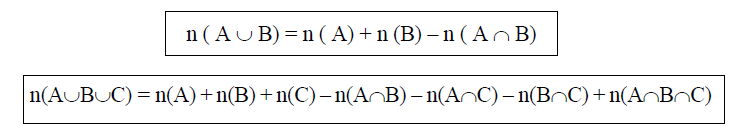
Contoh:








Demikian penjelasan sederhana tentang teori dasar himpunan dan beberapa contoh soal dan pembahasan yang sudah pernah dikeluarkan dalam seleksi masuk perguruan tinggi negeri.
Via : http://www.foldersoal.com

Belum ada Komentar untuk "Teori Dasar Himpunan dan Beberapa Contoh Soal "
Posting Komentar